참조
https://www.youtube.com/watch?v=XepXtl9YKwc
1. 의미
- Maximum likelihood를 찾았다?
- 관측치에 대한 우도를 최대화 하는 평균 or 표준편차를 찾은것
- 데이터의 분포를 fit하기 위한 최적의 방법(분포)를 찾는 것
2. 예시
- Goal: 쥐의 몸무게들을 잘 표현하는 분포 찾기
- 어떤 분포가 가장 적합한지?
- 가장 간단한 정규분포로 가정
- 평균 활용
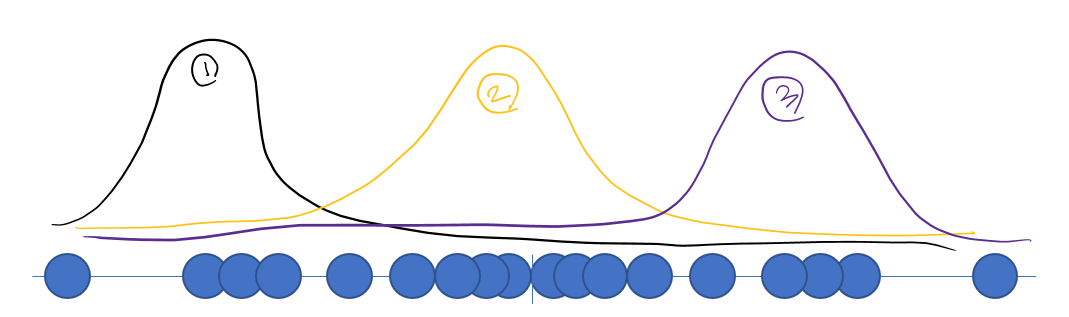
- 원: 쥐의 몸무게 데이터, 그래프: 가정할 분포
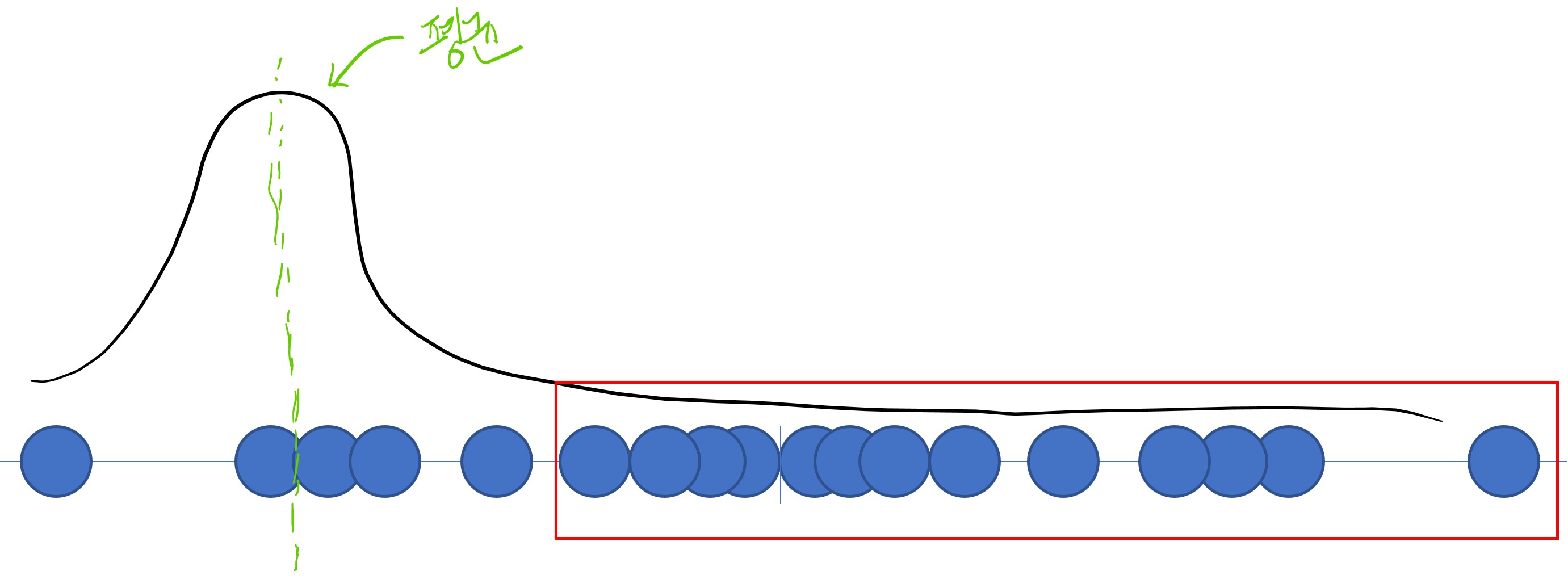
- 1번, 3번 분포의 경우
- 평균과 거리가 먼 오른쪽/왼쪽 데이터들의 likelihood는 낮게 평가됨
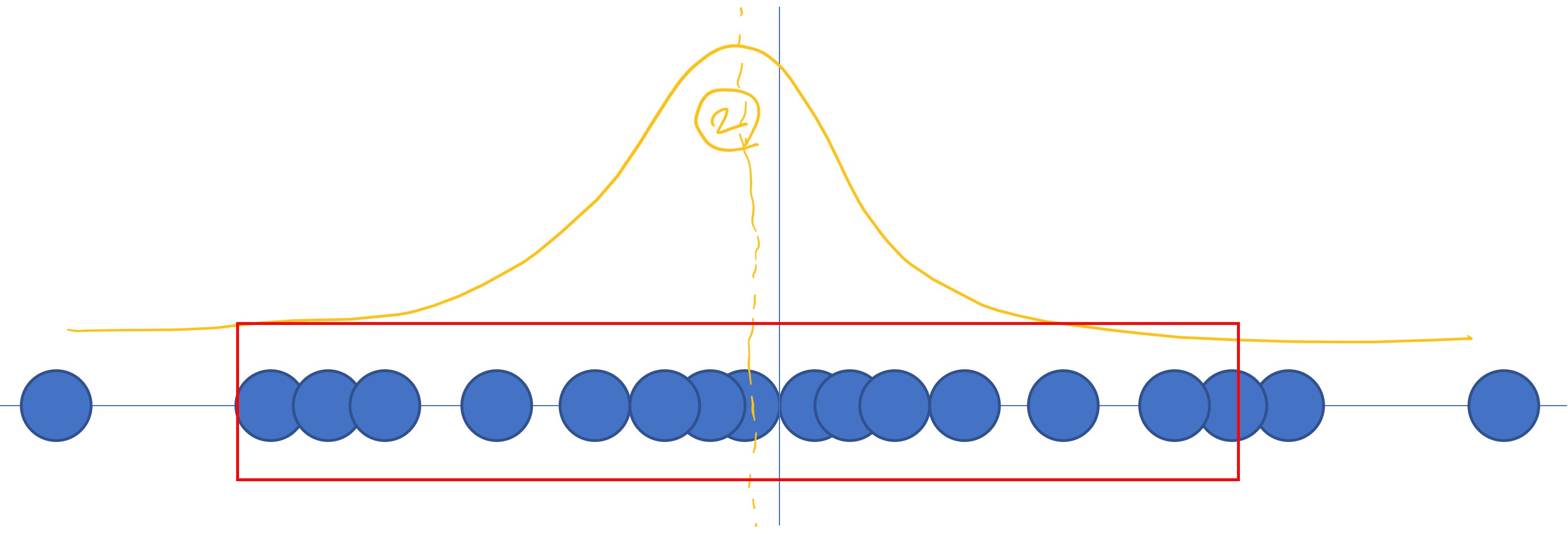
- 2번 분포의 경우
- 가정한 분포의 평균과 데이터의 평균이 일치
- likelihood가 높게 평가됨
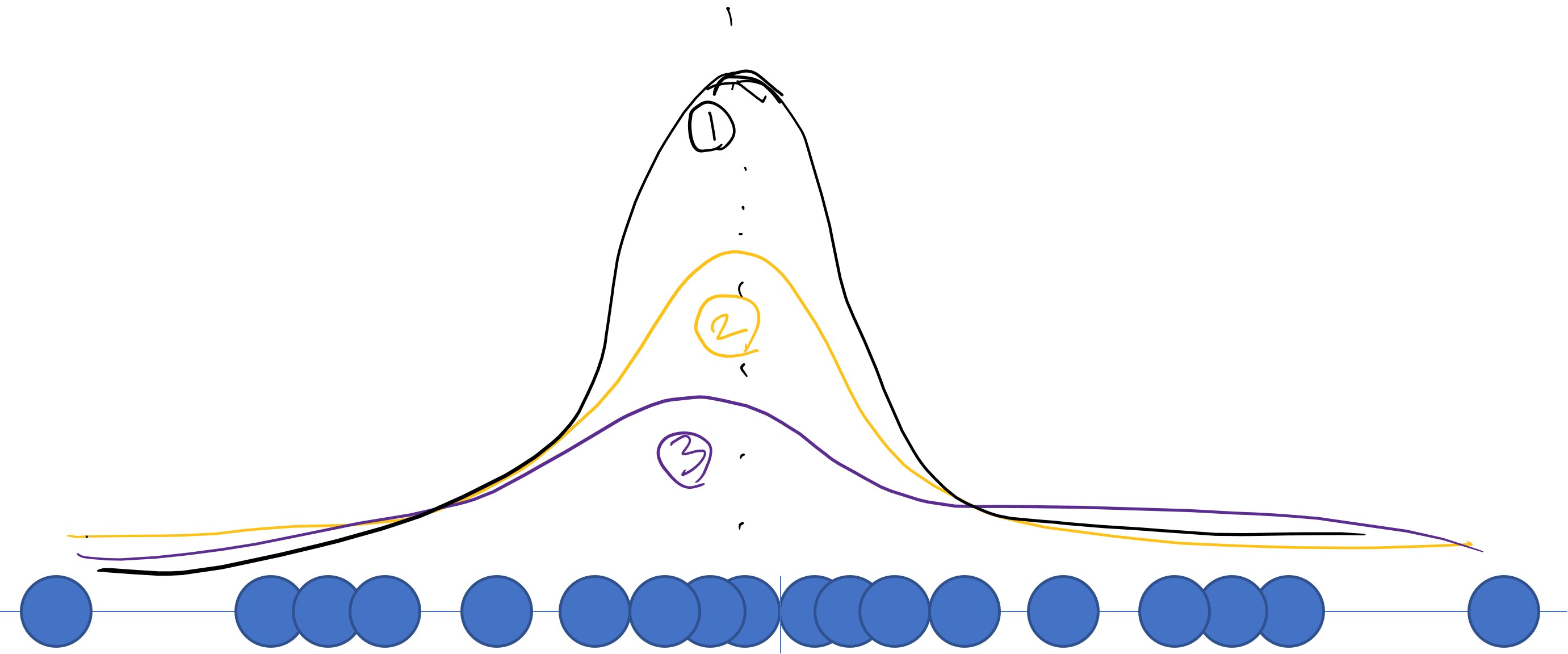
- 표준편차 활용
- 표준편차가 커질수록 분포가 퍼짐
- 평균과 동일하게 표준편차에 따라 likelihood값이 달라짐
- likelihood가 최대가 되는 표준편차를 선택
3. 딥러닝과의 관계
- 모델의 가중치 $\theta = (W^1,…,W^L)$
- 소프트맥스 벡터=카테고리분포의 모수 $(p_1,…,p_K)$ 를 모델링
- 정답 레이블 $y=(y_1,…,y_K)$ (원핫 인코딩)을 이용, 소프트맥스 벡터의 로그가능도를 최적화
- $\hat{\theta_{MLE}}=argmax_{\theta}({1 \over n} \sum_{i=1}^n \sum_{k=1}^K y_{i,k} log(MLP_\theta (x_i)_k))$
- 소프트맥스 벡터의 likelihood를 최적화
- Log likelihood를 사용하는 이유
- 계산의 편의성
- 추정한 분포와 데이터의 거리의 곱으로 가능도를 표현하기 때문에, 그 값의 크기를 줄일 수 있음