1. Entropy

• 의미?
  • 정보를 표현하는데 필요한 (평균) 최소 자원량
  • 공통 단위로 표현할수 없을까?
    • 정보이론의 아버지 (Claude Elwood Shannon)
    • Bits! 로 표현해라!
      • 몇개의 비트로 표시할 수 있는가?!
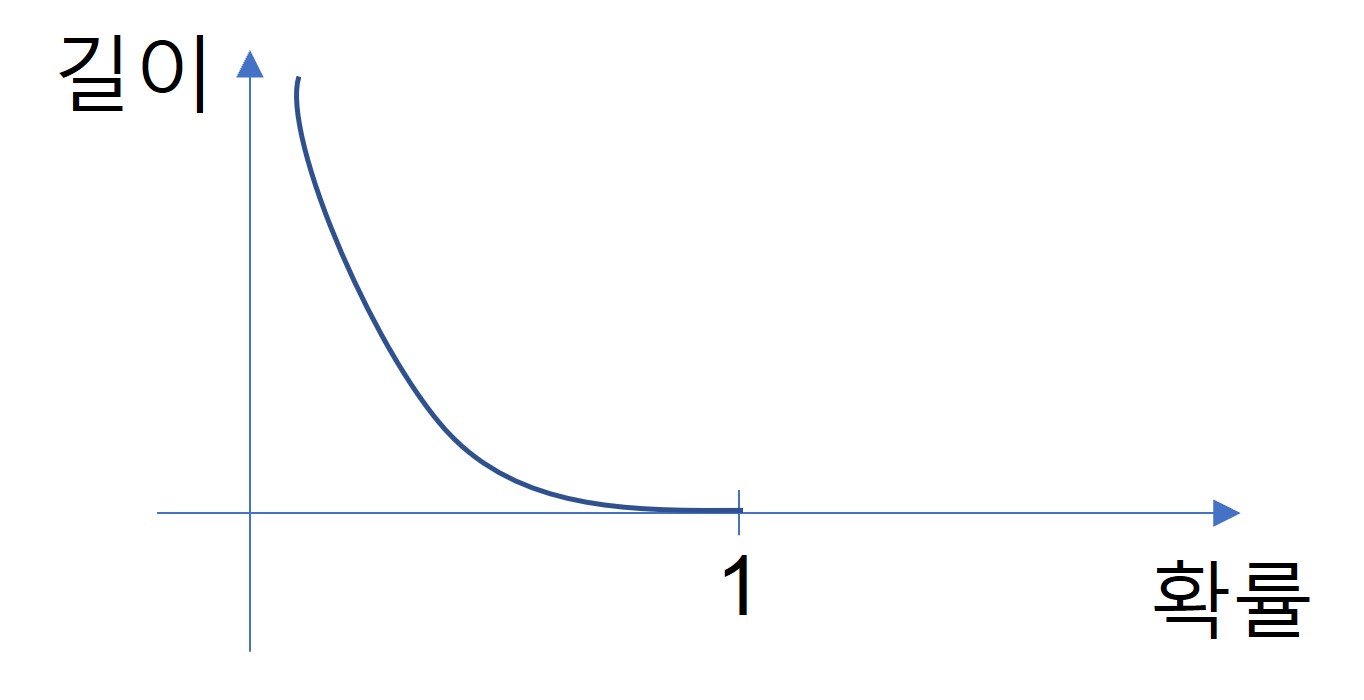
• 확률에 따라, 낮은 것를 길게, 높은 것을 짧게
  • -log 함수와 동일한 형태 그래프
  • $ -log_2 P_i $ : 길이
  • $\sum_i P_i(-log_2 P_i)$ : 기대값이 최소 평균 길이가 됨
    • 정보이론의 아버지가 증명했음!
• 확률이 Uniform하면 Entropy가 최대가 됨

2. Cross Entropy

• $ \sum_i P_i(-log_2 Q_i) $
  • $ Q_i $ : 내가 생각한 확률!

3. KL Divergence

• $ -\sum_i P_i(-log_2 Q_i) + \sum_i P_i(-log_2 P_i)$
  • 내가 생각한 확률이 비효율 적인 정도!
• 학습을 통해 Q_i를 효율적인 P_i로 근사시키는데 사용됨!

4. Mutual information

• $ \sum_i \sum_j P(x_i, y_i) log {P(x_i, y_i) \over P(x_i)P(y_i)} $
  • 실제론 독립이 아닌데, 독립이라고 생각했을때, 비효율 적인 정도!
• 즉! Mutual information이 크면 x와 y 관계가 있는것
• 독립이면 log값이 0이되기 때문!
• 독립?
  • $ P(x_i \vert y_i) = {P(x_i, y_i) \over P(y_i)} $
  • $ P(x_i \vert y_i) = P(x_i)P(y_i) $

5. Machine learning 활용

• Entropy: 불확실성의 정도 (값이 낮을 수록 불확실성 낮음)
  • class 개수에 따라
    • $4개: 0 <= Entropy <= 2$
    • $8개: 0 <= Entropy <= 3$
    • $16개: 0 <= Entropy <= 4$
• Decision Tree
  • 중요한 특징을 앞쪽에서 구분
  • 확실이 구분이 된다 = 불확실성이 낮다 = Entropy 낮다
• Active learning
  • 이미 만든 모델을 개선시키고 싶을때,
  • Entropy 활용
    • 새로운 데이터 추가
    • 일정 수치 이상의 Entropy 데이터만 레이블링
    • 기존의 학습 데이터에 추가
      • 잘 모른 데이터만 추가해 학습 가능
      • 훈련 데이터 관리의 효율적