Batch Normalization layer

KyungHyun Lim

ML/AI/SW Developer

Jul 31, 2021

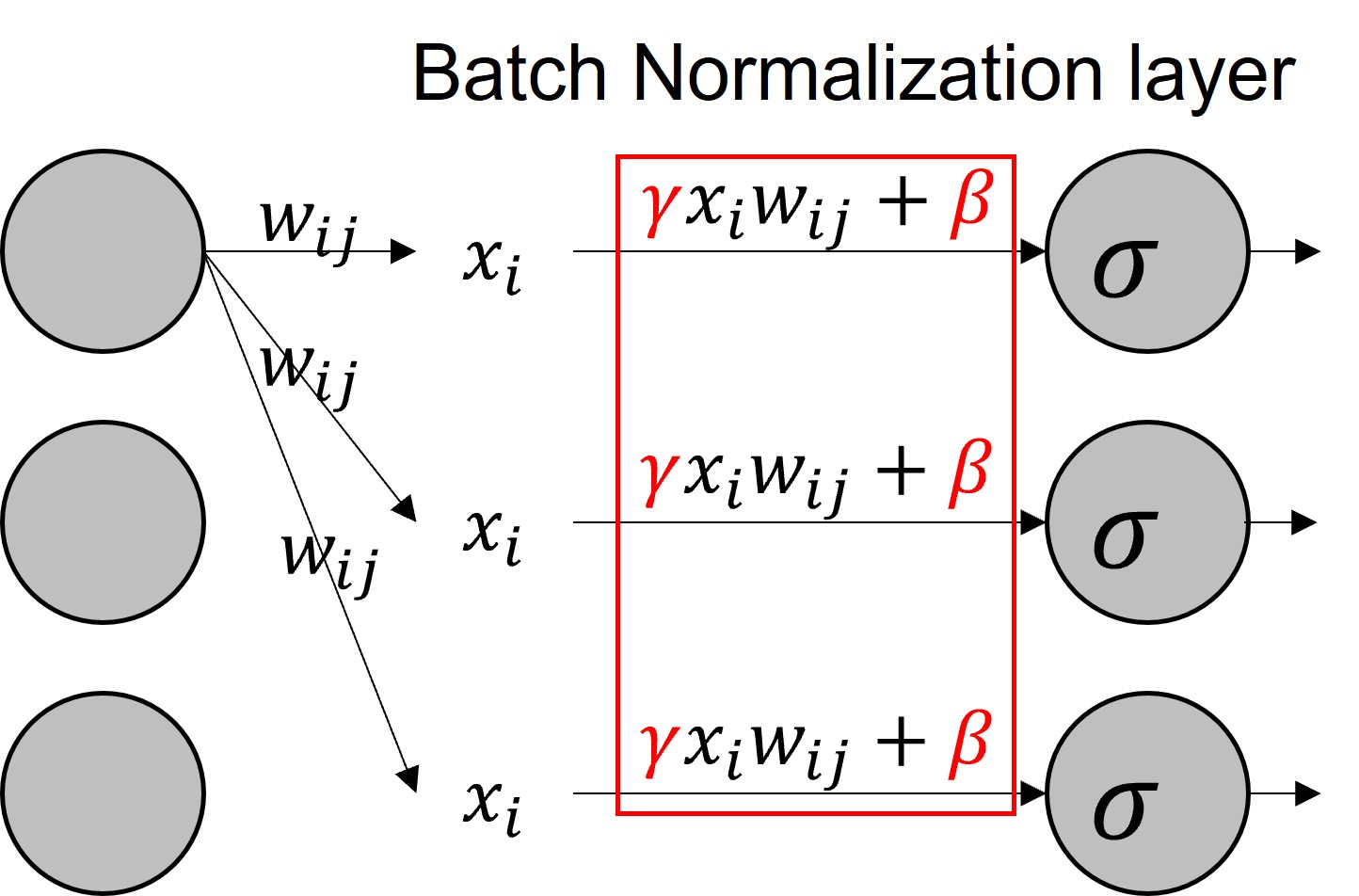
Annotation
- $x_i$ : 다음 레이어에 들어가려는 입력, 0 <= i <= batch_size
- $w_{ij}$ : 해당 노드의 가중치, 0 <= i, j <= # of layer
- $\sigma$ : 활성화 함수
- $\gamma , \ \beta$ : Batch norm layer에서 학습하는 파라미터
동작 순서
1. 평균 $\mu_B$ : 미니배치에 대한 평균
2. 분산 $\sigma_B^2$ : 미니배치에 대한 분산
3. Normalize = ${x_i-\mu_B \over \sigma_B} = \hat x_i$
  - 평균 0, 분산 1인 분포를 따르게됨
4. $\gamma \hat x_i + \beta = y_i$
5. $y_i$ : batch norm layer의 결과물
$=> \sigma (BN(xw))$
Test 시에는?
- 총 데이터수 / 배치수 만큼의 $\gamma , \ \beta$ 존재
- 이 값들의 평균 활용
  - m: 미니배치의 수
  - moving average
    - simple: 일반적인 평균
    - exponential: 가중치를 부여해서 나중에 구한 값에 가중치를 더줌 (과거의 값을 잊어버린다. = 초기 학습 값은 부정확하다)
  - $E[\mu_B] $
  - $E[\sigma_B^2] \times {m \over m-1}$
    - $E[{1 \over m} \sum_{i=1}^m (x_i-\mu_B)^2] = {(m-1) \sigma_{real} \over m }$
    - biased estimator
    - 데이터 전체의 평균과 분산과 같아진다!
CNN 에서는?
- 같은 filter = 같은 $\gamma , \ \beta$
  - 즉, 필터 개수만큼의 $\gamma , \ \beta$ 존재
- $m \times p \times q$ samples!
  - $(p, q)$ : 출력 크기

Batch안의 데이터마다 $x_i$ 값이 일정하지 않음
- 즉, $x_i$ 가 랜덤하다고 볼 수 있음 (랜덤분포)
평균과 분산을 구해 빼고 나누어주고, 학습한 파라미터를 다시 곱하고 더해줌
- Randomvariable : 랜덤하게 퍼져있는 알갱이들
- Normalize 단계 까지 : 한군데로 모아줌
- 마지막 단계 : 다시 뿌려줌!
- 어디어 어떻게 뿌릴까를 학습하는 것!
활성화 함수가 Sigmoid 라면?
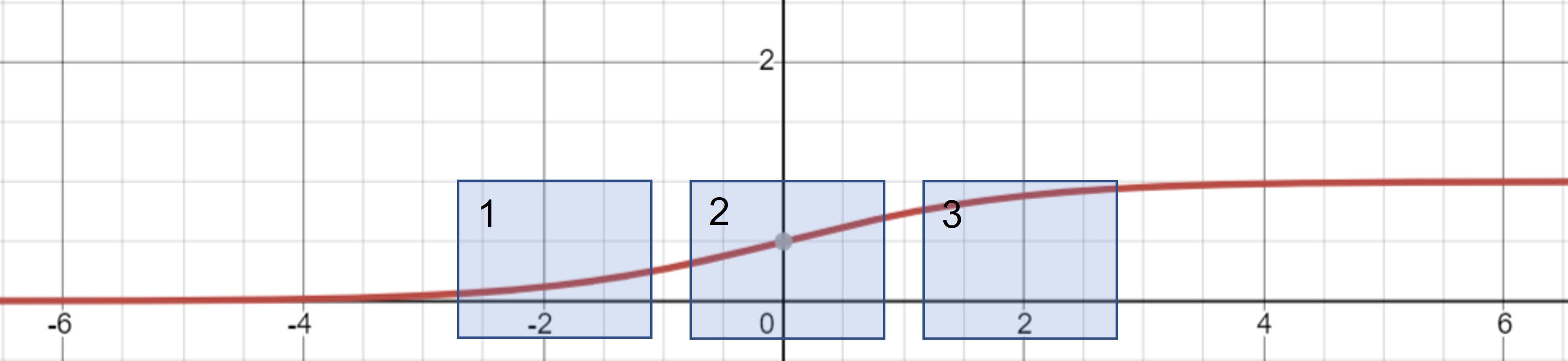
- 2번에 뿌려준다면? 거의 선형함수와 동일, 비선형성을 잃어 버릴 수 있음
- 너무 끝에 치우쳐 뿌려준다면? gradient가 없음
- 즉, 적절하게 뿌려주기 위한 학습
  - 1, 2 번 영역
  - 비선형성이 존재하고, gradient 또한 적정수준 존재!
딥러닝 모델이 적절한지 파악하는 방법
- $\gamma , \ \beta$ 의 초기 값: 1, 0 근처
- 0 근처에서 뿌려보면서 loss가 작아지는 방향으로 결정
  - 시작점을 조절해 유도가능
효과!
- vanishing gradient 보완 가능
- 빠른학습 (논문에 따르면 14배)
- learning rate 키워도 된다!
- Dropout이 필요 없음