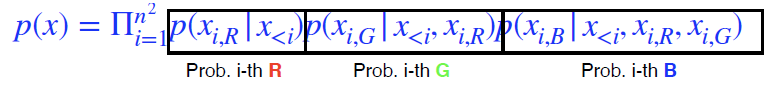1. Intro

• Richard Feynman(1918 ~ 1988)
  What i cannot create, i do not understand.
• Generative model을 학습 시킨다는 것은?
  • 일반적으로 이미지, 문장 등의 데이터를 생성하는 모델을 만들어 내는것이라고 생각하지만, 더 많은 의미를 포함한다!
  • Generation (sampling) $x_{new} \sim P(x)$
  • Density estimation (anomaly detection)
    • $P(x)$ 는 만약 x가 원하는 것(E.g. 이미지면 강아지)과 같으면 값이 높을 것이다.
    • Explicit model: 생성뿐아니라 무엇을 생성하는 지 알고 있다.
  • Unsupervised representation learning (feature learning)
    • E.g. ears, tail, etc!! 이미지의 특징

2. Statics

2.1 Basic Discrete Distributions

• Bernoulli distribution
  • $D = {Heads, Tails}$
  • $P(X=Heads)=p then P(X=Tails)=1-p$
  • $X ~ Ber(p)$ 로 표현
  • 한개의 숫자로 분포를 표현할 수 있음
• Categorical distribution
  • $D = {1,…, m}$
  • $P(Y=i)=p_i, such that \sum_{i=1}^m p_i = 1$
  • $Y~Cat(p_1, …, p_m)$ 로 표현
  • m-1개의 숫자로 분포를 표현할 수 있음(마지막 숫자는 1에서 나머지 합을 빼면 되기 때문)

2.2 Example: RGB의 결합 확률 분포 모델링

• $(r, g, b) \sim p(R,G,B)$
• 경우의 수 = 256 x 256 x 256
• 몇개의 파라미터가 필요?
  • 256 x 256 x 256 - 1 개
  • So. big $\leftarrow$ Too hard

2.3 Example: Binary의 결합 확률 분포 모델링

• $X_1,…,X_n \rightarrow n binary pixels$
• 경우의 수 = 2 x 2 x … x 2 = $2^n$
• 몇개의 파라미터가 필요?
  • $2^n$ - 1 개
  • So. big $\leftarrow$ Too hard
• 딥러닝에서 파라미터가 너무 많아지면 학습이 어렵워 성능 저하 우려가 있다.

2.4 파라미터를 줄이는 방법

• 가정: 모든 파라미터가 Independent 하다.
  • $P(x_1,…,x_n) = p(x_1)p(x_2)…p(x_n)$
  • 경우의 수 = 2 x 2 x … x 2 = $2^n$
  • 몇개의 파라미터가 필요?
    • n개
    • why?

      각각의 픽셀에 대해 1개의 파라미터만 있으면 되기 때문(각 파라미터들이 독립적이니까)
    

• Three important rules
  • Chain rule:
    • $P(x_1,…,x_m) = p(x_1)p(x_2 \vert x_1)p(x_3 \vert x_1,x_2)…p(x_n \vert x_1,…,x_{n-1})$
  • Bayes’ rule:
    • $P(x \vert y)={P(x,y) \over P(y)} = {P(y \vert x) P(x) \over p(y)}$
  • Conditional Independence(가정):
    • if $x \bot y \vert z, $ then $P(x \vert y,z) = P(x \vert z)$
    • z가 주어졌을 때, x와 y가 independent하다면, y는 상관이 없다.

2.5 Chain rule + Conditional Independence

• Chain rule
  • 필요한 파라미터수?
    • $P(x_1)$ : 1개
    • $P(x_2 \vert x_1)$ : 2개 ( $P(x_2 \vert x_1=0), P(x_2 \vert x_1=1)$ )
    • $P(x_3 \vert x_1, x_2)$ : 4개
    • $1+2+…+2^{n-1} = 2^n - 1$
  • Why? 달라진게 없으니까…
• Chain rule + Conditional Independence
  • Markov 가정. 바로 이전 값에만 Indenpendent 하다.
    • $x_{10} \bot x_9, \ x_9 \bot x_8, \ …$
  • Markov 가정을 적용한 Chain rule
    • $P(x_1,…,x_m) = p(x_1)p(x_2 \vert x_1)p(x_3 \vert x_2)…p(x_n \vert x_{n-1})$
    • 이쁘게 바뀐다!
  • 몇개의 파라미더 필요? 2n-1 개

3. Models

3.1 Auto-regressive Model

• 28x28 binary pixels
• $P(x)=P(x_1,…,x_784) over x \in {0,1}^{784} $
• $P(x)$ 를 어떻게 parametieze 할 수 있을까?
  • Chain rule을 이용해 결합 확률분포 생성
  • 이것을 autoregressive model이라 부름
    • 이전 n개를 고려 $\rightarrow$ AR(n) 모델
  • 모든 random variable들의 순서가 필요

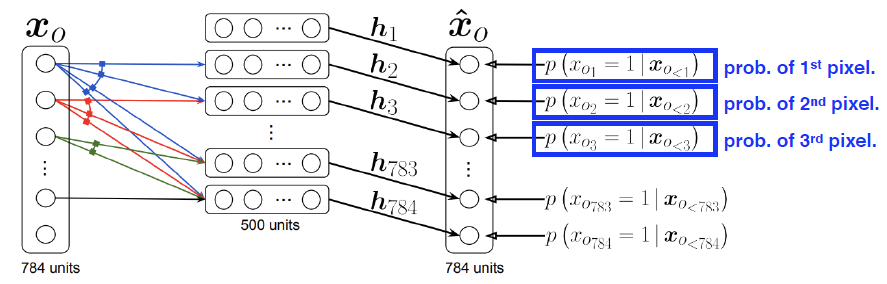
3.2 NADE: Neural Autoregressive Density

• $P(x_i \vert x_{1:i-1} = \sigma(a_ih_i + b_i) \ where \ h_i=\sigma (W_{<i}x_{1:i-1} + c)$
• i번째 픽셀을 1~i-1번째 까지 dependent하게 설정
• explicit 모델
  • How? 결합확률분포가 다음과 같이 계산될 수 있다.
    • $P(x_1,…,x_{784}) = P(x_1)P(x_2 \vert x_1)…P(x_{784} \vert x_{1:783})$
  • 어떤 입력에 대한 확률을 계산을 할 수 있다.
• Conitnuous한 데이터의 경우 Gaussian mixture 모델을 활용

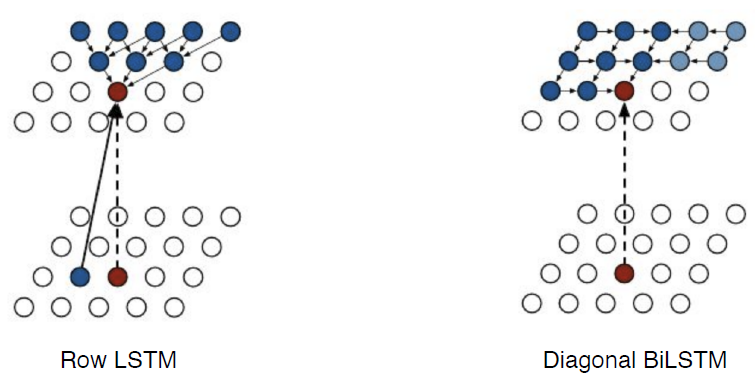
3.3 Pixel RNN

• Ordering
  
  • Row LSTM: i번째 위쪽에 있는 정보를 활용
  • Diagonal BiLSTM: 이전 정보들을 모두 활용

4. 한줄 정리

Generative 모델이 많이 쓰이는 GAN, VAE 와 같이 Generation을 할 수 있는 모델 뿐만이 아니라, 확률 값을 계산할 수 있는 explicit한 모델들 또한 존재한다!