BLEU score가 번역 문장 평가에 있어서 갖는 단점은 무엇이 있을까요?
1. Beam search
1.1 Greedy decoding
- 다음에 나올 단어로 가장 확률이 높은 단어만으로 학습을 하는 것
- 즉, 가장 좋아보이는 단어를 그때 그때 선택하는 greedy 형태
- 한번 잘 못 선택하면 뒤로 돌아갈 수 없음
1.2 Exhaustive search
- $P(y \vert x) = P(y_1 \vert x)P(y_2 \vert y_1, x)… $
- 전체적인 문장의 확률을 고려할 수 있음
- 하지만 디코더의 각 time step마다 $V^t$ 개의 가능한 경우의 수를 검토해야함, 이것은 시간복잡도가 $O(V^t)$ 로 매우 비효율적
1.3 Beam search
- Greedy와 Exhaustive의 사이에 있는 방법
- Core idea: 정해진 k개 경우의 수(hypothesis)만 검토하는 방법
- 보통 5~10개
- $score(y_1, …, y_t)=logP_{LM}(y_1,…,y_t \vert x)= \sum_{i=1}^t logP_{LM} (y_t \vert y_1, …,y_{i-1},x)$
- log => 단조증가, 큰값은 log를 취해도 다른 수에비해 큰값으로 유지됨
- 매 time step 마다 k개 tracking
- Process
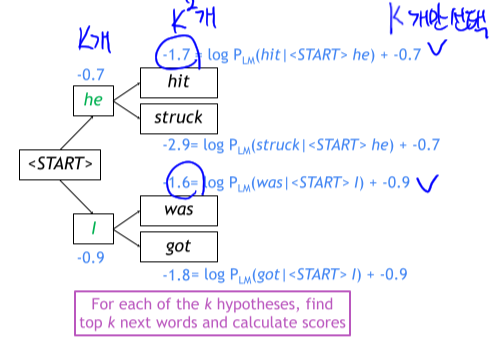
- 확률이 높은 K개의 단어 선택
- 즉, 매 time step마다 K^2개의 후보만 searching 후 확률이 가장 높은 K개의 후보만 선택
- hypothesis들이 각각 다른 시점에서 < END > 를 생성할 수 있음
- 다른 시점에 생성에 종료됨
- 또는 Stopping criterion을 활용해 강제 종료 가능
- 상대적으로 길이가 길수록 joint probability가 작아짐
- 각 hypothesis 별로 단어의 길이로 나누어 주어 공평하게 비교
2. BLEU score
2.1 단순한 비교방식

- 자리와 단어를 비교하는 방식으로 정확한 평가가 어려움
- E.g
- GT: I Love you
- Pred: oh I Love you
- 위와 같은 경우 score는 0
- Recall
- 소환해야 하는 대상중에 얼마나 잘 소환했는가…
- 평균
- 산술평균: 일반 평균
- 기하평균: 곱해서 루트
- 조화평균: 역수의 산술 평균의 역수
- 산술 >= 기하 >= 조화
- 조화평균은 작은쪽에 더 가중치가 있는 평균
- F-score => 조화평균으로 Precision과 Recall을 계산
2.2 BLEU score
- N-gram overlap
- I love this movie very much
- 나는 이 영화를 많이 사랑한다.
- (정말)이 없지만, 충분히 괜찮은 번역임 -> Recall을 고려하지 않는 이유
- $BLEU = min (1, \ {length \ of \ prediction \over length \ of \ reference }) (\prod_i^n precision_i)^{1/n}$
- 기하평균
- reference보다 짧은 문장을 생성했을 때, 짧은 비율만큼 precision을 낮추어주고, 길게 생성했을 때는 1로 설정해 원하는 모든 단어가 있을 경우 100%을 기대할 수 있다.
- Examples

- model 1
- Precision (1-gram): 9개의 단어 중 Half, my, heart, is, in, ooh, na 7개의 단어 일치 $\rightarrow {7 \over 9}$
- Precision (2-gram): 8개의 단어 묶음 중 my heart, heart is, is in, ooh na 4개의 묶음 일치 $\rightarrow {4 \over 8}$
- Precision (3-gram): 7개의 단어 묶음 중 my heart is, heart is in 2개의 묶음 일치 $\rightarrow {2 \over 7}$
- Precision (4-gram): 6개의 단어 묶음 중 my heart is in 1개의 묶음 일치 $\rightarrow {1 \over 6}$
- Breviry penalty: reference는 10개 단어, model1은 9개의 단어를 생성했기 때문에 $\rightarrow {9 \over 10}$
- $ BLEU score = 0.9 \times ( {7 * 4 * 2 * 1 \over 9 * 8 * 7 * 6})^{1 \over 4} $
- model 2
- 모든 단어들은 동일하게 구성되어있지만, 2-gram 부터는 맞는 것이 없음
- $ BLEU score = 1 \times 0 $
- model 1
