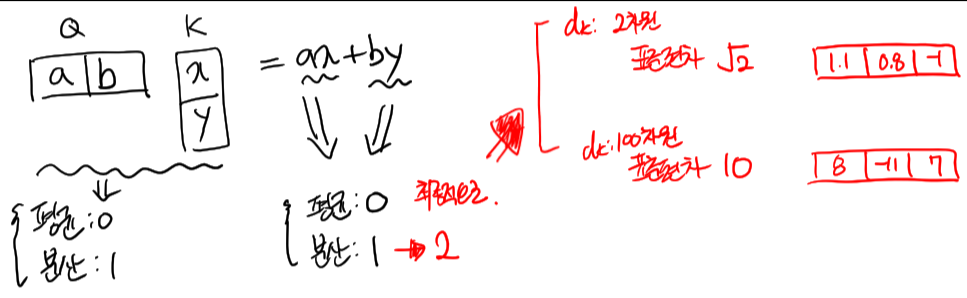1. RNN

1.1 Long term dependency

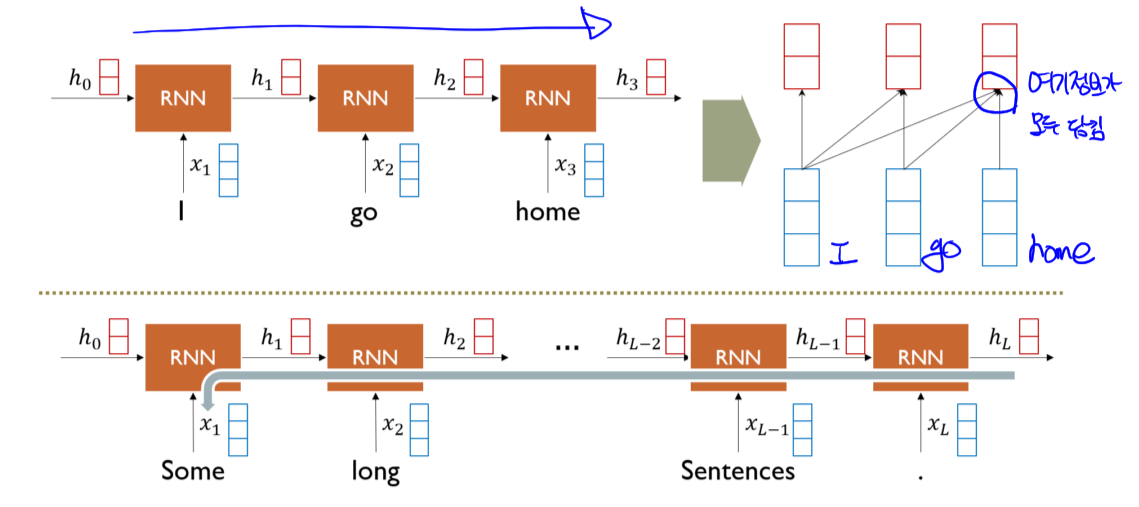
• $h_3$ 에 이전 정보들이 모두 담겨 시퀀스가 길어질수록 상대적으로 멀리있는 정보가 희미해짐
• Gradient vanishing/expoloding 문제도 발생

1.2 Bi-directional RNN

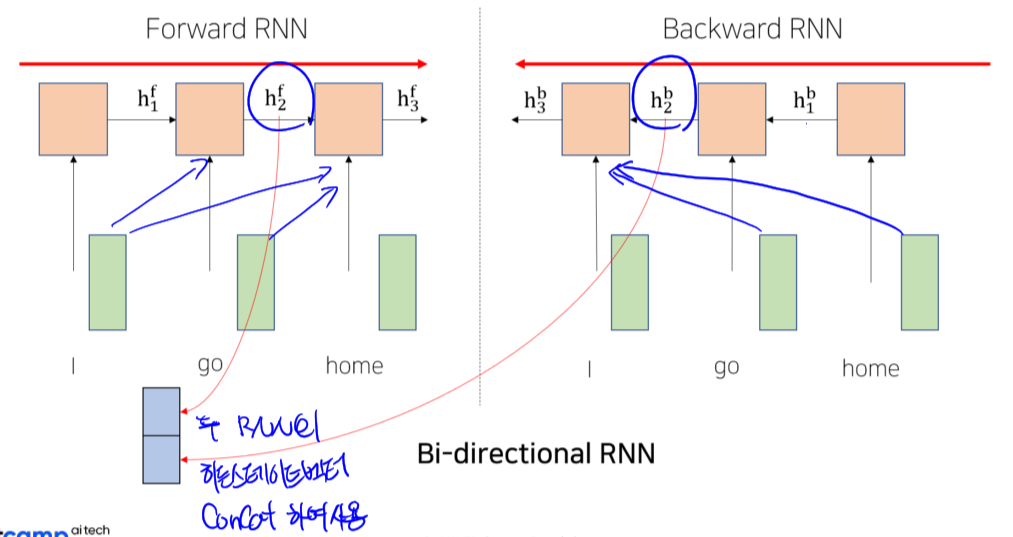
• Foward 방향과, Backward 방향 두개의 서로 다른 파라미터를 가지는 두 RNN을 활용
• 양방향의 hidden state 벡터를 concat하여 사용
• Long term dependency 어느정도 보완하려는 시도

2. Transformer

2.1 Self-attention 방식

• 과정
  
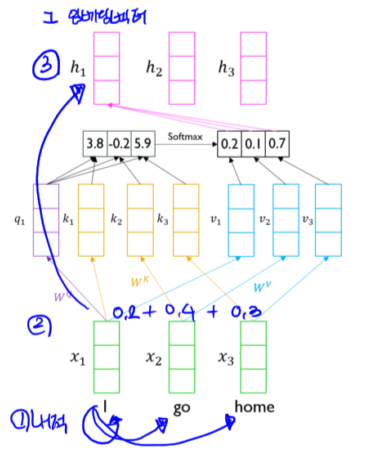
  1. 자기자신 및 나머지 워드들과 내적
  2. Softmax를 취해 가중치를 구하고 벡터에 곱하고 서로 더함
  3. 해당 워드에 대한 임베딩 벡터로 사용
• 문제점
  • 자기자신과 내적할 때, 더 큰 값을 가질 수 밖에 없음
  • 즉, 자기자신의 정보만을 주로 포함하고 있는 벡터가 됨
• 개선된 과정
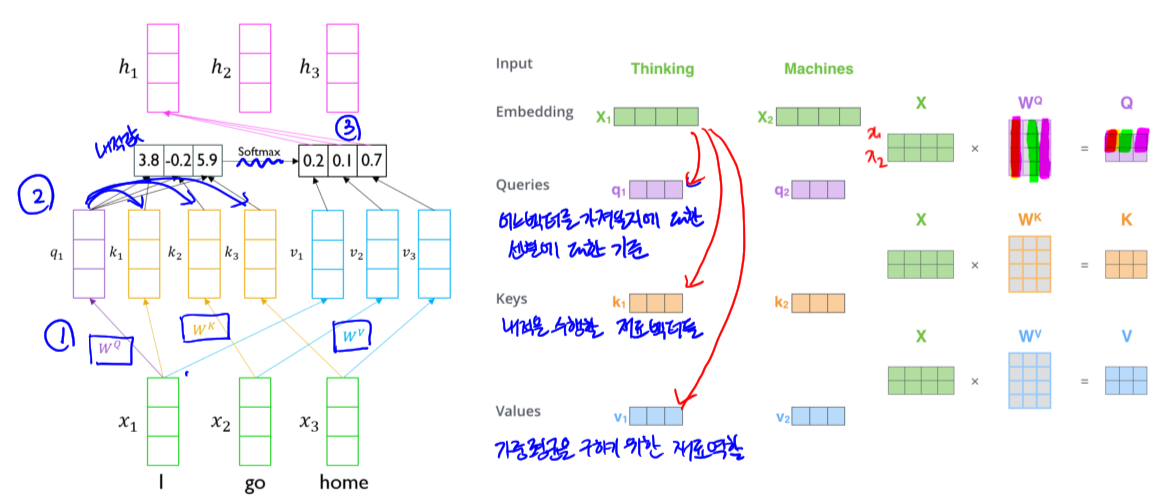
  1. $W^Q, \ W^K, \ W^V$ 를 이용해 각각 Query, Key, Value로 변환
  2. Query와 Key 벡터들을 내적 후 softmax를 취해 가중치 생성
  3. Value들에 가중치를 적용하고 더해 hidden state 벡터 생성
• 개선 사항
  • 자기 자신이 아닌 다른 워드와의 내적 값이 더 커질 수 있음
  • 즉, 더 유연한 임베딩 벡터를 생성할 수 있음
  • Time step이 멀어져도 정보를 유지 할 수 있음 (RNN에서의 개선사항)

2.2 Scaled Dot-Product Attention

• Self-attention 계산 과정
• 입력: Query(q), (Key(k), Value(v)) 페어 집합
• 출력: Weighted sum of Values
• Query와 key는 동일한 차원을 가져야함, Value는 가중평균을 구하기 위한 것으로 달라도 됨
• $A(q, K, V) = \sum_i {exp(q \cdot k_i) \over \sum_j exp(q \cdot k_j)}v_i$
  • ${exp(q \cdot k_i) \over \sum_j exp(q \cdot k_j)}$ : 가중치
  • $similarity * v_i$ : 가중평균으로 구해진 Attention vector
    
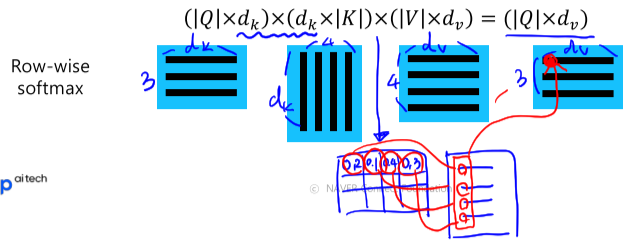
• Row-wise softmax 예시
  

2.3 Problems

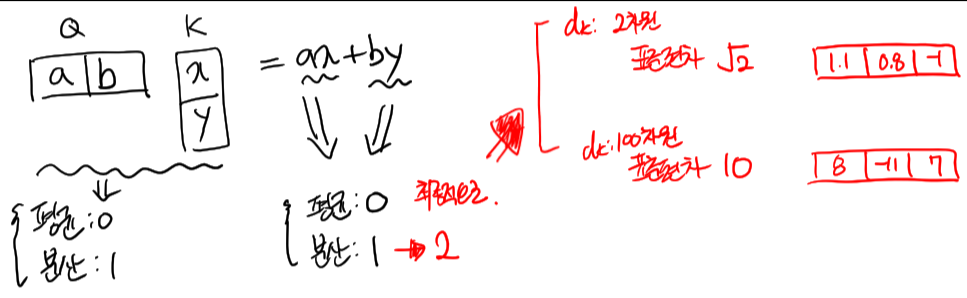
• $d_k$ 가 클수록, 분산과 표준편차가 커지고, soft-max를 취했을 때, 더 큰값에 몰리는 패턴이 나타남
  • $\sqrt {d_k}$ 로 나누어 주면서 영향을 적게하는 연산을 추가
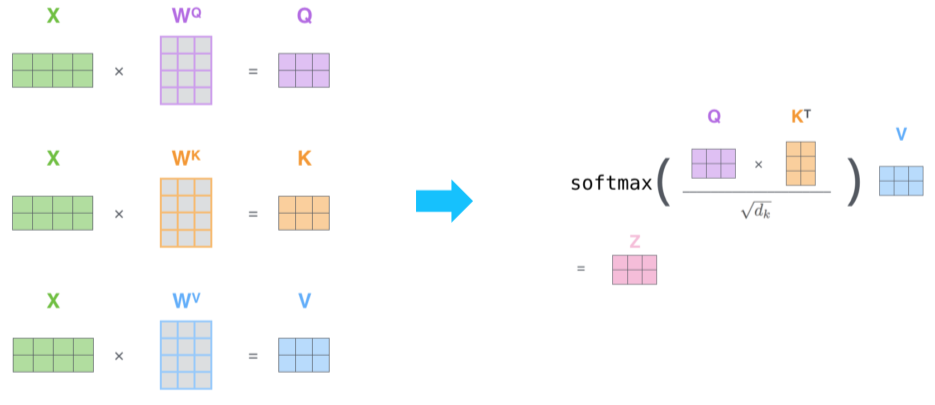
  • $A(Q,K,V)=softmax({QK^T \over \sqrt {d_k}})V$

3. 참고하기 좋은 사이트

• Attention
• Hugging face tutorial