1. Numpy / 벡터 & 행렬

1.1 Numerical Python - Numpy

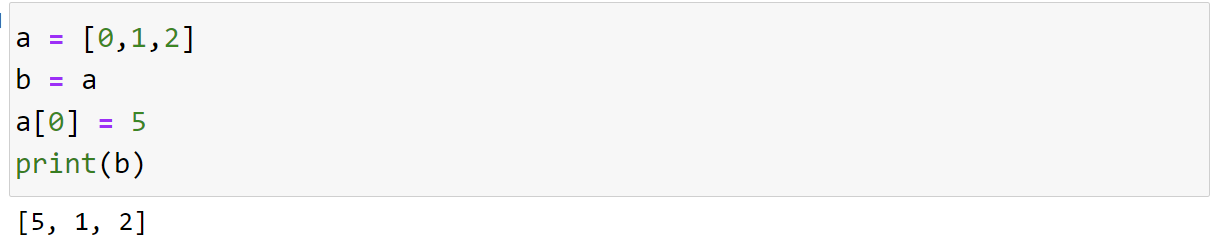
• 기본적으로 파이썬 리스트는 메모리 주소 복사
• fancy index

1.2 벡터란?

• 공간에서 한 점을 표현하는 것
• 기준점으로 부터의 상대적 위치
• Hadamard product: 성분 곱

  # Hadamard product
  np.array([1, 2, 3]) * np.array([4, 5, 6]) # = [4, 20, 18]
  

• norm
  • 기하학적 성질이 달라짐
  • L1 norm: Sum(변화량의 절대 값)
    • 마름모 꼴
    • Robust 학습, Lasso 회귀
  • L2 norm: 유클라디안 거리
    • 원
    • Laplace 근사, Ridge 회귀
    • 두 벡터의 각도 계산
      $ cos\theta = inner(x, y) / (L2(x) \times L2(y)) $
• 내적
  • 정사영된(orthogonal projection) 벡터의 길이
  • 두 벡터가 얼마나 유사한 패턴을 가지고 있는지

1.3 행렬이란?

• 벡터를 원소로 가지는 2차원 배열 (n개 행 r개열 벡터 => nxr)
  • 공간상의 여러 점들을 모아둔 것
• 전치행렬 (Transpose matrix) : 행 <=> 열
• 행렬곱을 통해 벡터를 다른 차원의 공간의 데이터로 변형 가능
• 역행렬은 행과 열 숫자가 같고 행렬식이 0이 아닌 경우에만 존재
  • 유사역행렬, Moore-Penrose 역행렬 A+를 이용
  • $ n>=m: A^+ = (A^TA)^{-1}A^T $
    • $ A^+A = I 만 성립 $
  • $ n<=m: A^+ = A^T(A^TA)^{-1} $
    • $ AA^+ = I 만 성립 $
  • numpy 활용

     np.linalg.pinv(Y) # 유사 역행렬
    

  • 응용1: 연립방정식 풀기
    • $ Ax = b => x = A^+b$
  • 응용2: 선형회귀 분석
    • $ X\beta = \hat y \approx y => \beta = X^+y $
    • L2 norm을 활용해 $ \hat y , y $ 근사가능

2. 경사하강법

2.1 기본

• 미분(differentialtion): 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구
  • $(x, f(x))$에서 접선의 기울기: 어느 방향으로 움직여야 값이 증가/감소 하는지 알 수 있음
  • 극값에 도달하면 최적화가 멈춤 => 미분 값이 0인 지점

   # 미분을 위한 파이선 라이브러리
   import sympy as sym
   from sympy.abc import x
  
   sym.diff(sym.poly(x**2 + 5*x + 6), x) # 해당 다항식을 x에 대해 미분하라S
  

• 편미분(partial differentiation)
  • 일부 변수에 대해서만 미분
    • $ f(x,y) = x^2 + y $
    • $ \partial x f(x,y) = 2x $
  • 변수가 벡터이면?
    • 그레디언트(gradient) 벡터 활용
    • $ \nabla{f} = (\partial{x_1}, … ,\partial{x_d}) $
    • $ -\nabla{f} $ 벡터를 그리면 극점으로 수렴

2.2 심화

• 선형회귀 목적식:
  • 아래식을 최소화하는 $\beta$를 찾음
  • $ \nabla \Vert y-X \beta \Vert _2 = (\partial _\beta{_1} \Vert y-X \Vert _2, …, \partial _\beta{_d} \Vert y-X \Vert _2) $
  • $ =-{X^T(y-X\beta) \over n\Vert{y-X\beta{^t}}\Vert{_2}} $
  • $ \beta{^{t+1}} \leftarrow \beta{^t}-\lambda{\nabla{_\beta{||y-X\beta{^t}||_2}}} $

     # lr: 학습률, T: 학습 횟수
     # 종료조건이 학습 횟수
     for t in range(T):
      e = y - X @ beta
      gradient = - transpose(X) @ e
      beta = beta - lr * gradient
    

  • 경사하강법 사용시 학습률과, 학습 횟수를 매우 적절하게 선택해야 최적으로 수렴할 수 있음
• convex 함수(볼록 함수)가 아닌 경우 다른 경사하강법이 필요
  • Stochastic gradient descent(SGD) 확률적 경사하강법
    • $\theta{^{t+1}}\leftarrow \theta{^t}-\hat{\nabla{_\theta \mathcal{L}(\theta{^t})}}$
    • mini batch를 활용
    • 일부의 데이터로 조금씩 이동하므로 Non convex 함수에서 보다 효과적
  • 하드웨어의 메모리적 한계도 보완 가능