1. pandas 1 / 딥러닝 학습방법

1.1 pandas 1

• 기본적인 pandas 라이브러리 사용법
• 데이터 접근
  • loc => 인덱스 이름을 사용해 접근
  • iloc => 인덱스 번호로 접근
• inplace: 원본에 적용 유무(True/False)
• describe: 전체적인 통계값
• 데이터 가공

 # 1. apply
 f = lambda x : x.max() - x.min()
 df.info.apply(f) # 데이터 프레임의 column 별로 결과값 반환

 # 2. applymap
 f = labmda x : -x
 df.applymap(f).head(5) # 처음  \sim  5개 element에만 적용

1.2 딥러닝 학습 방법

• 비선형모델인 신경망 중심!
• 기본적인 선형 모델 수식
  • O: output, X: data, W: weight, b: bias
  • $ O = X W + b $
• Softmax: 모델의 출력을 확률로 해석할 수 있도록 해주는 연산

 def softmax(x):
     d = np.exp(x - np.max(x, axis=-1, keepdims=True)) # 오버플로우 방지
     n = np.sum(d axis=-1, keepdims=True) # 전체 합
     val = d / n
     return val

• activation function
  • 선형 $\rightarrow$ 비선형 변환
    • activation function을 사용하지 않으면 딥러닝도 선형모델과 다를 것이 없음
  • 가장 많이 사용됬던 함수: sigmoid, tanh
  • 현재 인기: relu
• 층이 깊을수록 목적함수 근사를 위해 필요한 뉴런의 개수가 줄어듦 $\leftarrow$ 효율적으로 학습 가능
  • But, 최적화하기는 어려워 짐
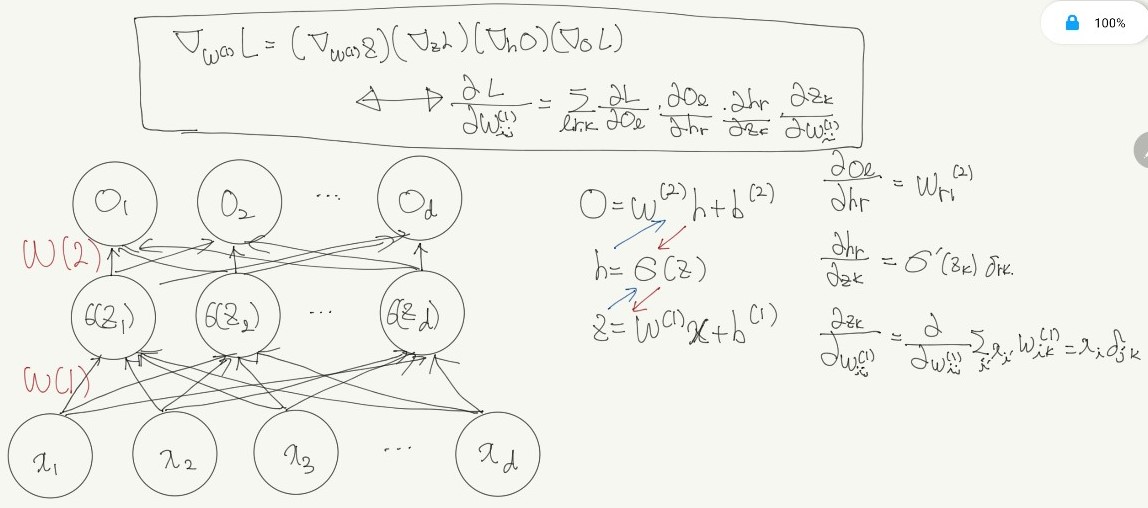
• 역전파(backpropagation) 알고리즘
  • 각 층 파라미터의 그레디언트 벡터는 윗층 부터 역순으로 계산됨
  • 연쇄법칙활용
    • ${ \partial z \over \partial x } = {\partial z \over \partial w} {\partial w \over \partial x} $
    • 2층 신경망의 역전파 알고리즘
      

2. pandas 2 / 확률론

2.1 pandas 2

• Groupby
  • split $\rightarrow$ apply $\rightarrow$ combine

  # 묶음의 기준이 되는 컬럼: Department
  # 적용받는 컬럼: salary
  # 적용받을 연산: mean
  df.groupby("Department")["salary"].mean()
  
  # 기준이 2개
  df.groupby("Department", "year")["salary"].mean()
  

  • filer: 특정 조건으로 데이터 검색

  df.groupby("Department").filter(lamda x: x["salary"] >=300)
  

• pivot_table
• crosstab
• Db connection 기능 제공

 import sqlite3
 # 데이터 베이스 연결
 con = sqlite3.connect("db경로")
 cur = con.cursor()
 cur.execute("SQL 쿼리 문")
 results = cur.fetchall()

 # 쿼리를 이용해 dataframe 생성
 df = pd.read_sql_query("SQL 쿼리 문", con)

2.2 확률론

• 확률론이 필요한 이유
  • 딥러닝은 확률론 기반 이론을 바탕으로 둠
  • L2-norm은 예측오차의 ‘분산’을 최소화하는 방향으로 학습
  • cross-entorpy는 모델 예측의 ‘불확실성’을 최소화 하는 방향으로 학습
• 이산확률변수 vs 연속확률변수
  • 이산확률변수
    • 모든 경우의 수를 고려, 확률을 더해 모델링
    • $ \mathbb{P} (X \in A ) = \sum_{x \in A} P(X=x) $
  • 연속확률변수
    • 데이터 공간에 정의된 확률변수의 밀도(pdf) 위에서 적분을 통해 모델링 (누적확률분포)
    • $ \mathbb{P} (X \in A ) = \int_{x \in A} P(X)dx $
• 주변확률분포
  • 결합확률분포 $ P(X, y) \sim \mathfrak{D} $ 에서,
  • $ P(X) $ 는 입력 X에 대한 주변확률 분포
    • y에 대한 정보는 부재
    • $ \sum_{y} P(X,y) $ / $ \int_{y} P(X,y)dy $
• 조건부확률분포
  • 입력 X와 출력 y사이의 관계를 모델링
  • $ P(X \mid y) \rightarrow $ y일때 X일 확률
  • $ P(y \mid X) \rightarrow $ 입력이 X일때 출력이 y일 확률
• 기계학습
  • 분류 문제에서 $ softmax(W \phi + b) $ 는 x로 부터 추출된 특징패턴 $ \phi (x) $ 와 가중치행렬 W를 통해 조건부 확률 $ P(y \mid X) $ 계산
  • 회귀 문제의 경우 조건부 기대값 $ \mathbb{E} [y \mid X] $ 를 추정
    • L2-norm을 최소화하는 함수와 동일
    • 목적에 따라 다른 통계량 사용가능
      • median 등
• 기대값?
  • 데이터를 대표하는 통계량 (평균)
    • $ \mathbb E_{X \sim P(\mathcal X)} [f(X)] = \int_{\mathcal X} f(X)P(\mathcal X)dX $
    • $ \mathbb E_{X \sim P(\mathcal X)} [f(X)] = \sum_{x \in \mathcal X} f(x)P(\mathcal X) $
  • 분산, 첨도, 공분산 등 여러 통계량 계산 가능
    • $ \mathbb{V} (X)=\mathbb{E}_{X \sim P(X)} [(X-\mathbb{E}[X])^2] $
    • $ Skewness(X)=\mathbb{E}[({X-\mathbb{E}[X] \over \sqrt{\mathbb{V}(X)}})^3] $
    • $ Cov(X_1, X_2)=\mathbb{E}_{X_1, X_2 \sim P(X_1, X_2)}[(X_1 - \mathbb{E}[X_1])(X_2 - \mathbb{E}[X_2])] $
• 몬테카를로 샘플링
  • 데이터의 확률분포를 모르는 경우 사용, 샘플링을 통해 기대값 계산
  • 이산/연속 상관없이 동작
  • 독립추출만 보장된다면 law of largenumber에 의해 수렴성 보장
  • $ \mathbb E_{X \sim P(X)}[f(X)] \approx {1 \over N} \sum_{i=1}^N f(x^i),\ x^i \sim^{i.i.d.} P(X) $