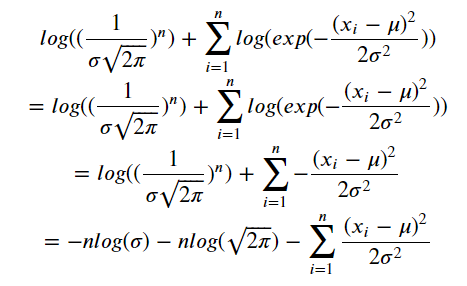1. 개인학습
- 파이썬 기초 3.1 ~ 7.2
- asterisk
print([1,2,3]) # [1,2,3] print(*[1,2,3]) # 1 2 3 => unpacking funtion((1,2,3,4,5)]) def function(*args): # 여러개 인자 print(args) # (1,2,3,4,5) print(*args) # 1 2 3 4 5 ** # keyword unpacking- Numpy, pandas 활용법
- 연구실에서 많이 했던것들
- numpy
- indexing, slicing, arrange …
- identity, eye
- diag: 대각선 값 추출
-
pandas
list_d = [1,2,3,4,5] list_s = pd.Series(list_d) #0 1 #1 2 #3 3 #4 4 #5 5
- AI 수학 기초 4 ~ 7
- 경사하강법
- 편미분(partial differentiation)
- 일부 변수에 대해서만 미분
- $ f(x,y) = x^2 + y $
- $ \partial x f(x,y) = 2x $
- 변수가 벡터이면?
- 그레디언트(gradient) 벡터 활용
- $ \nabla{f} = (\partial{x_1}, … ,\partial{x_d}) $
- $ -\nabla{f} $ 벡터를 그리면 극점으로 수렴
- 일부 변수에 대해서만 미분
- 선형회귀 목적식:
- 아래식을 최소화하는 $\beta$를 찾음
- $ \nabla \Vert y-X \beta \Vert _2 = (\partial _\beta{_1} \Vert y-X \Vert _2, …, \partial _\beta{_d} \Vert y-X \Vert _2) $
- $ =-{X^T(y-X\beta) \over n\Vert{y-X\beta{^t}}\Vert{_2}} $
- $ \beta{^{t+1}} \leftarrow \beta{^t}-\lambda{\nabla{_\beta{\Vert y-X\beta{^t}\Vert_2}}} $
- convex 함수(볼록 함수)가 아닌 경우 다른 경사하강법이 필요: SGD
- 편미분(partial differentiation)
- 통계
- 표본 평균: ${1 \over n}[x_1 + x_2 + …]$
- 표본 분산: ${1 \over n-1}[(x_1 - \mu)^2 + (x_2 - \mu)^2 + …]$
- MLE post 참조!
- 경사하강법
2. 과제풀이 4, 5번 마무리
- 4번
- “Good you win!” 을 출력해줘서 꼬인것이었다…
- 2시간 넘게 main test를 저것때문에…
- 5번
- 메인 함수 구현
- 크게 어려운점 없이 테스트 통과
3. 멘토시간 및 피어세션
- 강의 복습 (벡터 ~ 경사 하강법)
4. 선택과제 1
- 1번
- 선형회귀 구현해보기
- 목적함수 편미분! ```python _y = w*train_x + b
# gradient # w에 대한 편미분 # b에 대한 편미분 gradient_w = np.sum((w * train_x + b - train_y) * 2 * train_x) / n_data gradient_b = np.sum((w * train_x + b - train_y) * 2) / n_data
# w, b update with gradient and learning rate w = w - lr_rategradient_w b = b - lr_rategradient_b
# L2 norm과 np_sum 함수 활용해서 error 정의 error = np.mean(np.sum((_y - train_y)**2)) # Error graph 출력하기 위한 부분 errors.append(error)
* SGD로 구현하기! * 데이터 분할하기! * numpy index 활용 ```python batch_error = 0 # batch로 나누기 for batch in range(100): index = np.random.choice([i for i in range(1000)], size=10) batch_train_x = train_x[index] batch_train_y = train_y[index] _y = w*batch_train_x + b - 선형회귀 구현해보기
- 3번
- TODO 1
- TODO 2
- $\frac{\partial L(\theta \vert x)}{\partial \mu} = -\frac{1}{2\sigma^2}\sum_{i=1}^{n}\frac{\partial}{\partial \mu}\left(x_i^2-2x_i\mu+\mu^2\right) $
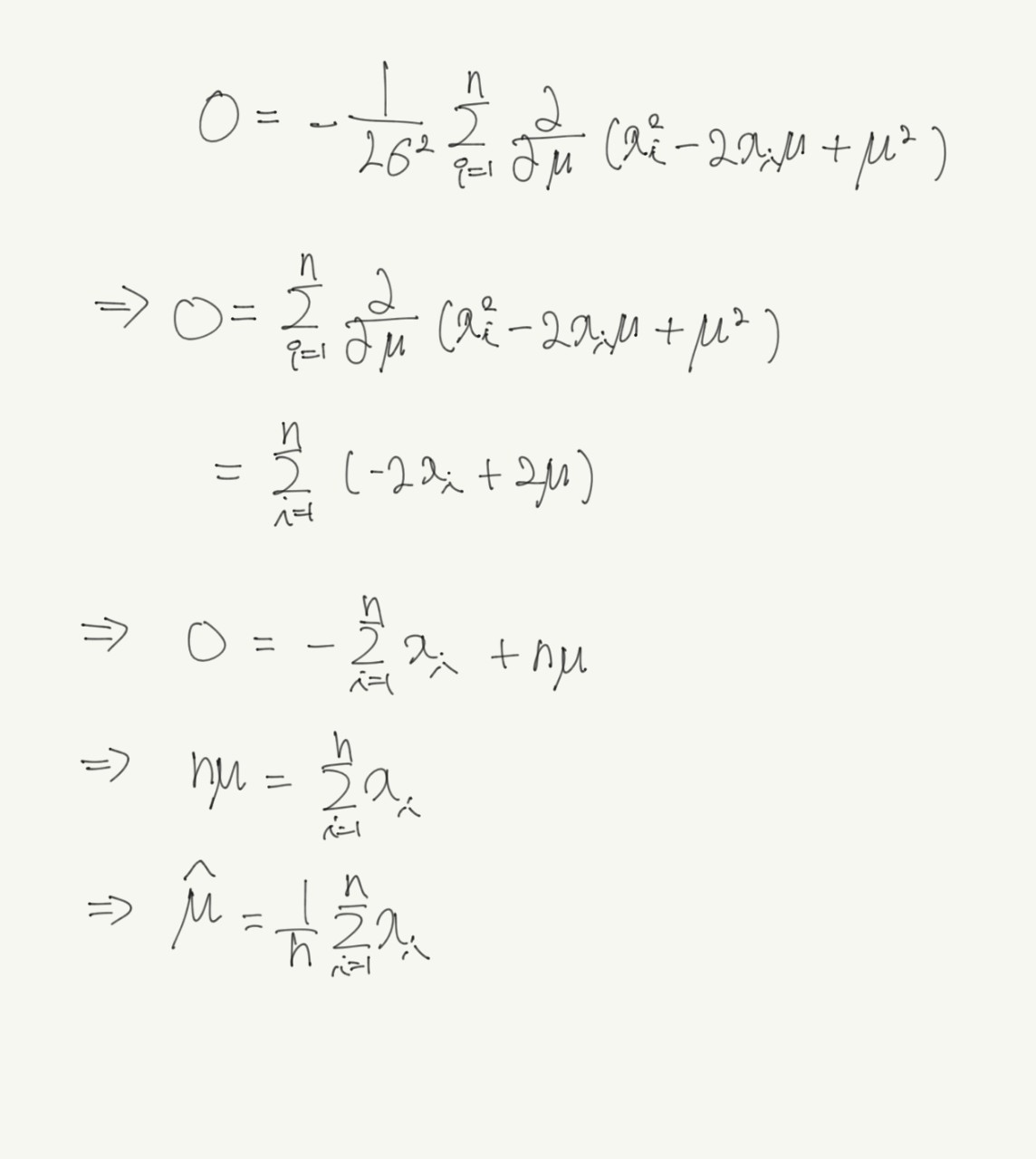
- TODO 3
- $ \frac{\partial L(\theta \vert x)}{\partial \sigma} = -{n \over \sigma} + {1 \over \sigma^3} \sum_{i=1}^n(x_i - \mu)^2 $
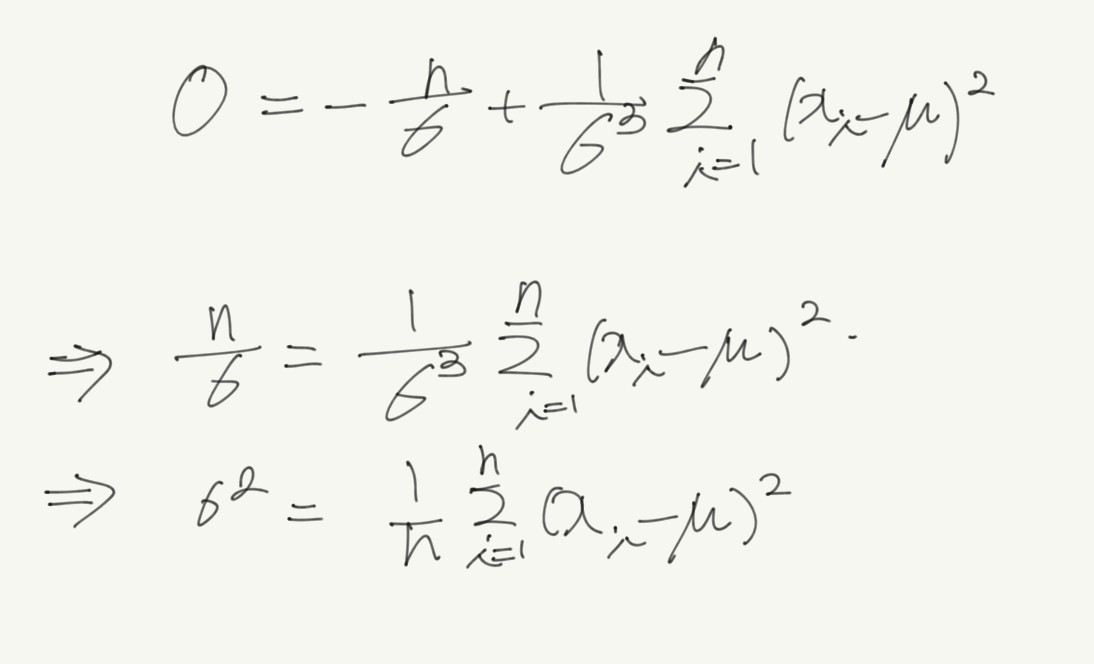
- TODO 1
5. 필수퀴즈 풀이
- 5강 - 계산실수…
- 6강, 7강, 9강